How To Find Sample Size Needed For Confidence Interval

Sample Size Calculator

Discover Out The Sample Size

This calculator computes the minimum number of necessary samples to meet the desired statistical constraints.

Confidence Level:
Margin of Error:
Population Proportion:		Use 50% if not certain
Population Size:		Exit blank if unlimited population size.

Detect Out the Margin of Error

This calculator gives out the margin of fault or confidence interval of observation or survey.

Confidence Level:
Sample Size:
Population Proportion:
Population Size:		Leave blank if unlimited population size.

In statistics, information is ofttimes inferred about a population by studying a finite number of individuals from that population, i.e. the population is sampled, and it is assumed that characteristics of the sample are representative of the overall population. For the following, it is assumed that at that place is a population of individuals where some proportion, p, of the population is distinguishable from the other 1-p in some way; e.g., p may be the proportion of individuals who take chocolate-brown hair, while the remaining one-p accept black, blond, red, etc. Thus, to estimate p in the population, a sample of n individuals could exist taken from the population, and the sample proportion, p̂, calculated for sampled individuals who have brownish pilus. Unfortunately, unless the full population is sampled, the estimate p̂ well-nigh probable won't equal the true value p, since p̂ suffers from sampling noise, i.e. information technology depends on the particular individuals that were sampled. However, sampling statistics can be used to calculate what are chosen conviction intervals, which are an indication of how close the judge p̂ is to the truthful value p.

Statistics of a Random Sample

The uncertainty in a given random sample (namely that is expected that the proportion estimate, p̂, is a good, but not perfect, approximation for the true proportion p) can be summarized by saying that the estimate p̂ is ordinarily distributed with hateful p and variance p(1-p)/n. For an explanation of why the sample approximate is unremarkably distributed, written report the Key Limit Theorem. As divers below, confidence level, confidence intervals, and sample sizes are all calculated with respect to this sampling distribution. In brusque, the confidence interval gives an interval around p in which an guess p̂ is "likely" to be. The confidence level gives simply how "likely" this is – e.g., a 95% confidence level indicates that it is expected that an judge p̂ lies in the confidence interval for 95% of the random samples that could be taken. The conviction interval depends on the sample size, n (the variance of the sample distribution is inversely proportional to n, meaning that the estimate gets closer to the truthful proportion equally north increases); thus, an acceptable fault rate in the guess tin can besides be set, chosen the margin of fault, ε, and solved for the sample size required for the called conviction interval to exist smaller than eastward; a calculation known every bit "sample size calculation."

Conviction Level

The confidence level is a measure of certainty regarding how accurately a sample reflects the population being studied within a chosen conviction interval. The most unremarkably used conviction levels are 90%, 95%, and 99%, which each have their own corresponding z-scores (which tin can be found using an equation or widely available tables like the ane provided below) based on the chosen confidence level. Note that using z-scores assumes that the sampling distribution is normally distributed, every bit described to a higher place in "Statistics of a Random Sample." Given that an experiment or survey is repeated many times, the confidence level essentially indicates the percentage of the fourth dimension that the resulting interval found from repeated tests volition contain the true result.

Conviction Level	z-score (±)
0.70	i.04
0.75	1.15
0.80	ane.28
0.85	1.44
0.92	i.75
0.95	1.96
0.96	2.05
0.98	2.33
0.99	2.58
0.999	iii.29
0.9999	3.89
0.99999	iv.42

Confidence Interval

In statistics, a conviction interval is an estimated range of probable values for a population parameter, for case, 40 ± 2 or twoscore ± 5%. Taking the commonly used 95% conviction level as an example, if the same population were sampled multiple times, and interval estimates made on each occasion, in approximately 95% of the cases, the true population parameter would be contained within the interval. Note that the 95% probability refers to the reliability of the estimation procedure and not to a specific interval. In one case an interval is calculated, it either contains or does not comprise the population parameter of interest. Some factors that bear on the width of a confidence interval include: size of the sample, conviction level, and variability within the sample.

There are different equations that can be used to summate confidence intervals depending on factors such as whether the standard divergence is known or smaller samples (n<xxx) are involved, among others. The calculator provided on this page calculates the conviction interval for a proportion and uses the following equations:

where

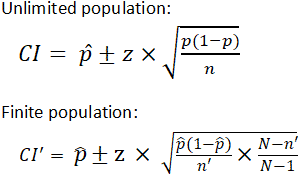
z is z score
p̂ is the population proportion
n and n' are sample size
Due north is the population size

Within statistics, a population is a ready of events or elements that have some relevance regarding a given question or experiment. Information technology can refer to an existing group of objects, systems, or even a hypothetical grouping of objects. Most normally, however, population is used to refer to a group of people, whether they are the number of employees in a company, number of people within a certain age group of some geographic area, or number of students in a academy'southward library at any given time.

Information technology is important to annotation that the equation needs to exist adapted when considering a finite population, as shown above. The (North-north)/(North-i) term in the finite population equation is referred to as the finite population correction cistron, and is necessary because it cannot exist assumed that all individuals in a sample are independent. For example, if the study population involves 10 people in a room with ages ranging from 1 to 100, and one of those chosen has an historic period of 100, the side by side person called is more likely to have a lower age. The finite population correction factor accounts for factors such as these. Refer below for an example of calculating a confidence interval with an unlimited population.

EX: Given that 120 people work at Company Q, 85 of which drink coffee daily, observe the 99% confidence interval of the truthful proportion of people who drink java at Company Q on a daily basis.

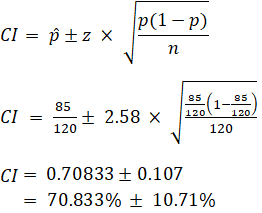
Sample Size Calculation

Sample size is a statistical concept that involves determining the number of observations or replicates (the repetition of an experimental status used to guess the variability of a phenomenon) that should be included in a statistical sample. It is an important aspect of any empirical study requiring that inferences be fabricated most a population based on a sample. Essentially, sample sizes are used to represent parts of a population chosen for whatsoever given survey or experiment. To conduct out this calculation, prepare the margin of mistake, ε, or the maximum altitude desired for the sample guess to deviate from the true value. To practise this, use the confidence interval equation above, but set the term to the correct of the ± sign equal to the margin of error, and solve for the resulting equation for sample size, n. The equation for calculating sample size is shown below.

where

z is the z score
ε is the margin of error
Due north is the population size
p̂ is the population proportion

EX: Make up one's mind the sample size necessary to approximate the proportion of people shopping at a supermarket in the U.Southward. that identify as vegan with 95% conviction, and a margin of fault of 5%. Assume a population proportion of 0.five, and unlimited population size. Remember that z for a 95% confidence level is 1.96. Refer to the table provided in the confidence level section for z scores of a range of conviction levels.

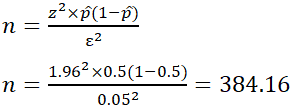
Thus, for the case above, a sample size of at least 385 people would be necessary. In the above example, some studies gauge that approximately vi% of the U.S. population identify as vegan, so rather than assuming 0.5 for p̂, 0.06 would be used. If it was known that 40 out of 500 people that entered a particular supermarket on a given day were vegan, p̂ would then exist 0.08.